Cogito ergo sum. René Descartes
Quantum Fisher information matrix and multiparameter estimation
Jing Liu, Haidong Yuan, Xiao-Ming Lu and Xiaoguang Wang
Journal of Physics A: Mathematical and Theoretical 53, 023001 (2020).
DOI: 10.1088/1751-8121/ab5d4d
Topical review for the special issue "Quantum multiparameter estimation and metrology".
Citations > 12 in Google Scholar Citations.
Journal of Physics A: Mathematical and Theoretical 53, 023001 (2020).
DOI: 10.1088/1751-8121/ab5d4d
Topical review for the special issue "Quantum multiparameter estimation and metrology".
Citations > 12 in Google Scholar Citations.
Quantum Fisher information matrix (QFIM) is a core concept in theoretical quantum metrology due to the significant importance of quantum Cramér–Rao bound in quantum parameter estimation. However, studies in recent years have revealed wide connections between QFIM and other aspects of quantum mechanics, including quantum thermodynamics, quantum phase transition, entanglement witness, quantum speed limit and non-Markovianity. These connections indicate that QFIM is more than a concept in quantum metrology, but rather a fundamental quantity in quantum mechanics. In this paper, we summarize the properties and existing calculation techniques of QFIM for various cases, and review the development of QFIM in some aspects of quantum mechanics apart from quantum metrology. On the other hand, as the main application of QFIM, the second part of this paper reviews the quantum multiparameter Cramér–Rao bound, its attainability condition and the associated optimal measurements. Moreover, recent developments in a few typical scenarios of quantum multiparameter estimation and the quantum advantages are also thoroughly discussed in this part.
Control enhanced multi-parameter quantum estimationJing Liu and Haidong Yuan
Physical Review A 96, 042114 (2017). DOI: 10.1103/PhysRevA.96.042114 Citations > 27 in Google Scholar Citations. Citations > 15 in Web of Science. The algorithm is integrated into the package QuanEstimation. |
|
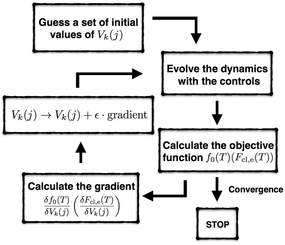
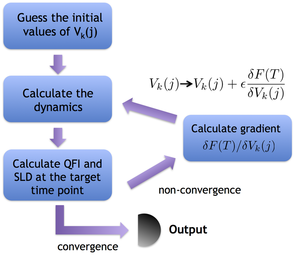
Most studies in multi-parameter estimation assume the dynamics is fixed and focus on identifying the optimal probe state and the optimal measurements. In practice, however, controls are usually available to alter the dynamics, which provides another degree of freedom. In this paper we employ optimal control methods, particularly the gradient ascent pulse engineering (GRAPE), to design optimal controls for the improvement of the precision limit in multi-parameter estimation. We show that the controlled schemes not only capable to provide a higher precision limit, but also have a higher stability to the inaccuracy of the time point performing the measurements. This high time stability will benefit the practical metrology where it is hard to perform the measurement at a very accurate time point due to the response time of the measurement apparatus.
|
Quantum parameter estimation with optimal control
Jing Liu and Haidong Yuan
Physical Review A 96, 012117 (2017). DOI: 10.1103/PhysRevA.96.012117 Citations > 35 in Google Scholar Citations. Citations > 21 in Web of Science. The algorithm is integrated into the package QuanEstimation. |
|
A pivotal task in quantum metrology, and quantum parameter estimation in general, is to design schemes that achieve the highest precision with given resources. Standard models of quantum metrology usually assume the dynamics is fixed, the highest precision is achieved by preparing the optimal probe states and performing optimal measurements. However, in many practical experimental settings, additional controls are usually available to alter the dynamics. Here we propose to use optimal control methods for further improvement on the precision limit of quantum parameter estimation. We show that by exploring the additional degree of freedom offered by the controls higher precision limit can be achieved. In particular we show that the precision limit under the controlled schemes can go beyond the constraints put by the coherent time, which is in contrast to the standard scheme where the precision limit is always bounded by the coherent time.
|
Quantum metrology with unitary parametrization processes
Jing Liu, Xiao-Xing Jing and Xiaoguang Wang
Scientific Reports 5, 8565 (2015). DOI: 10.1038/srep08565 Citations > 44 in Google Scholar Citations. Citations > 31 in Web of Science. |
|
Quantum Fisher information is a central quantity in quantum metrology. We discuss an alternative representation of quantum Fisher information for unitary parametrization processes. In this representation, all information of parametrization transformation, i.e., the entire dynamical information, is totally involved in a Hermitian operator H. Utilizing this representation, quantum Fisher information is only determined by H and the initial state. Furthermore, H can be expressed in an expanded form. The highlights of this form is that it can bring great convenience during the calculation for the Hamiltonians owning recursive commutations with their partial derivative. We apply this representation in a collective spin system and show the specific expression of H. For a simple case, a spin-half system, the quantum Fisher information is given and the optimal states to access maximum quantum Fisher information are found. Moreover, for an exponential form initial state, an analytical expression of quantum Fisher information by H operator is provided. The multiparameter quantum metrology is also considered and discussed utilizing this representation.
Quantum Fisher information for density matrices with arbitrary ranks
|
Jing Liu, Xiao-Xing Jing, Wei Zhong and Xiaoguang Wang
Communications in Theoretical Physics 61, 45-50 (2014). DOI: 10.1088/0253-6102/61/1/08 Citations > 72 in Google Scholar Citations Citations > 46 in Web of science Highlights of 2014 in Communications in Theoretical Physics. |
We provide a new expression of the quantum Fisher information (QFI) for a general system. Utilizing this expression, the QFI for a non-full rank density matrix is only determined by its support. This expression can bring convenience for an infinite-dimensional density matrix with a finite support.
|
Phase-matching condition for enhancement of phase sensitivity in quantum metrologyJing Liu, Xiao-Xing Jing and Xiaoguang Wang
Physical Review A 88, 042316 (2013). DOI: 10.1103/PhysRevA.88.042316 Citations > 98 in Google Scholar Citations. Citations > 74 in Web of Science. |
|
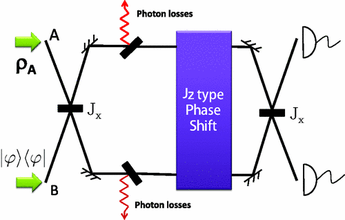
We find a phase-matching condition for enhancement of sensitivity in a Mach-Zehnder interferometer illuminated by an arbitrary state in one input port and an odd (even) state in the other port. Under this condition, the Fisher information becomes maximal with respect to the relative phase of two modes, and the phase sensitivity is enhanced. For the case with photon losses, we further find that the phase-matching condition remains unchanged with a coherent state and a coherent superposition state as the input states.
Nonunital non-Markovianity of quantum dynamics Jing Liu, Xiao-Ming Lu and Xiaoguang Wang
Physical Review A 87, 042103 (2013). DOI: 10.1103/PhysRevA.87.042103 Citations > 46 in Google Scholar Citations. Citations > 34 in Web of Science. |
|
Trace distance is available to capture the dynamical information of the unital aspect of a quantum process. However, it cannot reflect the nonunital part. So the nondivisibility originating from the nonunital aspect cannot be revealed by the corresponding measure based on the trace distance. We provide a measure of nonunital non Markovianity of quantum processes, which is a supplement to Breuer-Laine-Piilo non-Markovianity measure. A measure of the degree of the nonunitality is also provided.
